Yếu tố nào quyết định BẠN đạt điểm cao môn toán
Đề thi môn toán bao gồm bảy chuyên đề. Các câu được coi là dễ, cần ôn tập kỹ để lấy điểm tối đa đó là: khảo sát và vẽ đồ thị hàm số, số phức, tích phân và phương trình lượng giác. Sau đó hãy xác định những chuyên đề còn lại nào là thế mạnh của mình.

Môn Toán: Học sinh chỉ nháp ra giấy nội dung khó
Quan sát đề thi môn Toán trong những năm gần đây thấy thường có từ 2 đến 3 câu hỏi phân loại học sinh đòi hỏi các em cần có tư duy tổng hợp, còn lại các câu hỏi khác cơ bản bám sát nội dung chương trình các em được học.

Dạng bài tập dễ xuất hiện trong đề thi ĐH môn Toán
Trong đề thi đại học những năm gần đây, các dạng bài tập về hàm số, phương trình, bất phương trình, hệ phương trình số mũ Logarit… thường được đề cập tới. Các dạng câu hỏi học sinh dễ bị đánh “lừa” trong khi làm bài thi đại học, cao đẳng môn Toán.

Mẹo làm bài thi tốt nghiệp môn Toán đạt điểm cao
Năm nay, thí sinh lưu ý, thời gian thi tốt nghiệp môn Toán là 120 phút, đề thi chỉ hỏi vào các phần của lớp 12 song vẫn cần đến các kiến thức lớp dưới.

Gia sư toán 12 tại tp Vinh - PT mũ - logarit
Khi học xong bài này, ta sẽ biết được các phương pháp giải bất phương trình mũ và bất phương trình logarit. Đây là dạng toán nâng cao của dạng toán giải bất phương trình mũ và bất phương trình logarit.

Gia sư toán 12 tại Vinh - Khảo sát hàm số và ứng dụng đồ thị hàm số
- Vấn đề 1: Tìm cực trị của hàm số theo dấu hiệu I. - Vấn đề 2: Tìm cực trị của hàm số theo dấu hiệu II. - Vấn đề 3: Tìm cực trị hàm số chứa tham số. - Vấn đề 4: Tìm cực trị hàm số có điều kiện.

Gia sư toán lớp 12 tại TP Vinh - Đạo hàm và ứng dụng
- Giá trị lớn nhất, giá trị nhỏ nhất của hàm số - Cách tìm giá trị lớn nhất, giá trị nhỏ nhất trên một đoạn - Các ví dụ toán liên quan đến kháo sát GTLN, GTNN của hàm số
Gia sư toán 11 tại Vinh - Hai đường thảng vuông góc
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm và lần lượt song song với a và b.
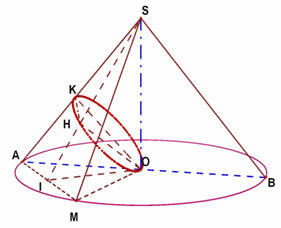
Tìm gia sư toán 11 tại Vinh - Vec tơ trong không gian
Trong không gian ba véc tơ gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng

Tìm gia sư toán 11 tại Vinh - Hai mặt phẳng song song
Phương pháp 2: Muốn chứng minh hai mặt phẳng song song, ta chứng minh mặt phẳng này chứa hai đường thẳng cắt nhau cùng song song với mặt phẳng kia.
Gia su toan 11 tai Vinh - Đường thẳng song song mặt phẳng
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SAB và I trung điểm của AB. Lấy điểm M trong đoạn AD sao cho AD =3AM. a. Tìm giao tuyến của hai mp (SAD) và (SBC)





.jpg)